Spring-loaded camming device

For flat-panel display manufacture, see S-LCD.

A spring-loaded camming device (also SLCD, cam or friend) is a piece of rock climbing or mountaineering protection equipment. It consists of three or four cams mounted on a common axle or two adjacent axles, so that pulling on the axle forces the cams to spread farther apart. The SLCD is used by pulling on the "trigger" (a small handle) so the cams move together, then inserting it into a crack or pocket in the rock and releasing the trigger to allow the cams to expand. At this point the climbing rope can be attached to a sling and carabiner at the end of the stem. A pull on the rope, such as that generated by a climber falling, will cause a properly placed SLCD to convert the pulling force along the stem of the unit into outwards pressure on the rock, generating massive amounts of friction and preventing the removal of the unit from the rock. Because of the large forces which are exerted on the rock when an SLCD is fallen on, it is very important that SLCDs are only placed in solid, strong rock.[1]

Contents

History

Vitaly Abalakov's invention of the Abalakov Cam was the first application to climbing of the principle of a constant-angle curved surface, with a cam shape based on the mathematical logarithmic spiral. Using a logarithmic spiral shape results in a constant angle between the cam and the rock at each contact point; this constant angle is designed to always provide the necessary friction to hold a cam in equilibrium.[2] Designed so that a load produces a rotational force, the logarithmic cam shape allowed for a single device to fit in a range of crack sizes without a change in the loading pattern, making it predictable and stable.

In 1973 Greg Lowe filed for a patent for a spring-loaded version of the Abalakov Cam.

Modern SLCDs were invented by Ray Jardine in 1978 (US patent 4,184,657) and sold under the brand name of "Friends".[3] Ray designed a spring-loaded opposing multiple cam unit with a more stable 13.75 degree camming angle and an innovative triggering mechanism. ("Friend" is now widely used by climbers to refer to SLCDs in general, but properly speaking it refers to the brand now manufactured by Wild Country.) Other popular brands include Black Diamond Camalots, Metolius Power Cams, DMM 4CUs, Trango FlexCams, and CCH Aliens.

Modern use

The invention of SLCDs revolutionized rock climbing because it meant that parallel or flared cracks could be protected. Furthermore, unlike pitons, SLCDs can be removed easily without causing damage to the rock, which made clean climbing (climbing without damaging the rock) practical on many more climbs. Since the invention of the Technical Friend (which replaces the original one-piece machined alloy shaft with a brazed assembly incorporating a length of thick stainless-steel cable, which is better able to cope with loading over an edge), there has been a great deal of development of the SLCD by a variety of manufacturers. For example, the adoption of the dual axle design by Black Diamond, the invention of three-lobed camming units to fit smaller cracks, and the more recent invention of the Link Cam by Omega Pacific, a design that allows one SLCD to span an even larger range of crack sizes. Behind the store display rack work done by companies such as Metolius Climbing help to keep cams safe in the market place and apply technical advances in their designs. SLCDs are sold in various sizes to fit a diverse range of cracks from about 6 mm to 300 mm wide, though devices of below about 10mm or above about 100 mm are not often seen.

Modern trad climbers often climb with numerous and variously sized SLCDs to cover a wide range of crack sizes, sometimes with duplicate units depending on protection requirements of the climb. Some crag climbs, such as those in Indian Creek, require numerous pieces of the same size as the crack maintains about the same size for the whole climb.

Engineering

For the purposes of this article, 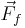\vec{F}_f=force of friction, 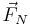\vec{F}_N=normal force, 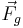\vec{F}_g=gravitational force in the case of a static force applied to the cam or applied force in the case of a fall, r=radius, \theta=camming angle, \mu=coefficient of friction between the SLCD and the rock, 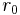r_0=r(0)=smallest radius of the camming lobe, C=a constant. We'll start by modeling the cam lobe as a 2-dimensional invincible bar of varying length r.

We need to find the relationship between the coefficient of friction and the angle. We'll do this by setting forces equal and such.

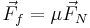
\vec{F}_f=\mu\vec{F}_N

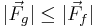
|\vec{F}_g|\le|\vec{F}_f|

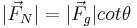
|\vec{F}_N|=|\vec{F}_g| cot\theta

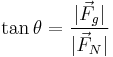
\tan\theta=\frac{|\vec{F}_g|}{|\vec{F}_N|}

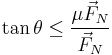
\tan\theta\le\frac{\mu \vec{F}_N}{\vec{F}_N}

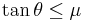
\tan\theta\le\mu

We also need to derive the spiral shape of the cam lobe keeping in mind that we want to maintain the same value of \theta as the rock wall gets further from the cam at the point of contact. Note that for this derivation, it does not matter whether the crack is closing, parallel, or flaring because we are only paying attention to the one point at which the cam comes in contact with the rock, which can only be further from or closer to the cam center. In order to derive the spiral, we will express the relationship between \theta and infinitesimal movements of the contact point.

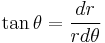
\tan\theta=\frac{dr}{rd\theta}

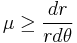
\mu\ge\frac{dr}{rd\theta}

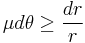
\mu d\theta\ge\frac{dr}{r}

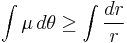
\int\mu\,d\theta\ge\int\frac{dr}{r}

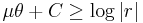
\mu\theta%2BC\ge \log|r|

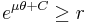
e^{\mu\theta%2BC}\ge r

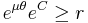
e^{\mu\theta}e^{C}\ge r

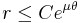
r\le Ce^{\mu\theta}

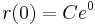
r(0)=Ce^{0}

C=r(0)

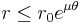
r\le r_0e^{\mu\theta}

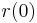But r cannot be less than r(0) by the definition of 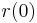r(0) since we do not have negative r values in this case, so

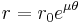
r= r_0e^{\mu\theta}

Note the graph of the spiral below from an angle of 0 to pi.

References

  1. ^ Cox, Steven M. and Kris Fulsaas, ed., ed (2003-09). Mountaineering: The Freedom of the Hills (7 ed.). Seattle: The Mountaineers. ISBN 0898868289. 
  2. ^ Duke SLCD research retrieved (2009-08-05)
  3. ^ Jardine, Raymond D. (1980-01-22), United States Patent: 4184657 - Climbing aids, http://patft.uspto.gov/netacgi/nph-Parser?Sect2=PTO1&Sect2=HITOFF&p=1&u=%2Fnetahtml%2Fsearch-bool.html&r=1&f=G&l=50&d=PALL&RefSrch=yes&Query=PN%2F4184657, retrieved 2009-12-21 

External links